=math
If you ever find yourself
transported to an alternate reality with a human society that has primitive
technology, which I assume must be fairly common based on stories I see,
perhaps you'd be tempted to introduce a positional number system.
Multiplication with, say, Roman numerals is quite slow, and I actually think
Arabic numerals were a key prerequisite for the Industrial Revolution in
Europe. But wait - have you ever observed kids learning arithmetic? It takes
people quite a while to learn arithmetic, and it would be much harder to
convince adults that memorizing a multiplication table with a bunch of
symbols they've never seen is a good use of their time. Is there something
easier to teach, that doesn't require as much memorization?
Alternatively, perhaps you're writing some fiction or making a TV show, and
want to show some foreign but internally consistent and logical number
system. Or, perhaps you're a wise-ass high school kid who resents math
teachers telling you to "show your work".
Here is a numeral system I
designed, which may be suitable for any of those cases. It's a
balanced ternary
system, which has several advantages:
- Base 3 has
the best radix economy.
- When adding many numbers, values tend to cancel out, reducing carries.
- Rounding
numbers can be done by truncation.
- Multiplication is simple and easy to
remember.
However, using a separate symbol for each trit is inefficient, with poor space efficiency, writing speed, and reading speed compared to a decimal system. So, I combine 3 trits into each symbol, trying to maximize writing speed, visual clarity, and space-efficiency. Different parts of the symbol represent the 3 trits, as follows:
- The left
end is [high/mid/low] for [+1/0/-1].
- The middle is
[loop/nothing/intersection] for [+1/0/-1].
- The right end is
[high/mid/low] for [+1/0/-1].
Here are all 27 resulting symbols, in order from -13 to +13:
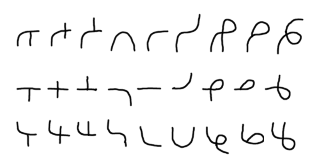
When doing long multiplication,
numerals could be used offset, with trits from different parts of numerals
on different rows being added together. Alternatively, multiplication could
be done using only the symbols for +1/0/-1, breaking up each numeral into 3
parts. At each row, a number being multiplied would be copied or inverted or
the row would be skipped.
Scientific notation is:
[exponent] [↑ or
↓] [additional significand precision]
The ↑ means the significand has a
leading +1, while ↓ means a leading -1. For example, (3^10)*(1 + 2/27) is
represented as:
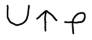
This format can be used without a
number on the right for approximate values. It could also be used with only
a number on the right, for fractional values close to 1.
With this
scientific notation system, a decimal point symbol is probably unnecessary,
but a vertical line could be used as a decimal point.
--:-:-:-:-----------------------------------:-:-:-:--
27 symbols (+1 with a decimal
point, +2 with arrows) is a suitable number of symbols for an alphabet. The
same set of symbols could thus be used for both numbers and letters. When
mixed with writing, numbers could be indicated by a leading zero.
Because numbers can be broken into trits, a primitive society with writing
slates but no paper could store numbers as wood beads fitting on a square
rod, each bead representing 1 trit by its rotation. A rod would be set down
on the unused 4th side, and trits could be read quickly from protrusions on
the other 3 sides, perhaps shifting beads along the rod to indicate
progress. (Historically, clay/wax tablets were used first, but the above
numeral system isn't designed for writing on those.)